Learning Math
Source: Dr. Trefor Bazett
Before Class
- 5 minute review before class
- Cover big points, i.e. big concepts
- Spaced Retrieval: pulling concepts back into memory to strengthen neural connections.
- Study Topics before class, preferably early in the day before class starts and right after you wake up (Dr. K)
- Previewing content, solidifying foundational concepts so you can focus on the time spent in class being more effective
Going to Class
- Being a stenographer is the worse possible thing to do
- Do more previewing so active learning is more available in class!!
- Tricks:
- Generate questions, write it down or circle a spot
- Annotate notes with stars, circles, question marks to look back on these concepts
Post-Class Review
- Go over notes in class, and try to make sure you 100% understood that content
- Reframing notes in your own words solidify understanding serves heavily in retaining information
- More Questions? Always come up with at least 3 questions
Most Important
- PRACTICE!
- Spend as much time as you can on this portion
- Concept Mapping!
- Write out main ideas of a particular subject in a big map
- Connecting ideas helps to strengthen understanding
Learning Effectively
- Growth Mindset
- A national experiment reveals where growth mindset improves achievement (Yeager, David S. et al)
- Positive and Negative mindsets inhibit developing improvments in metrics
- Fixed mindsets are bad!
- Metacognition (Dr. Sandra McGuire)
- When thinking about thinking/learning
- Pausing and reflecting on whether you’re learning effectively
- self-assessment
- Simplify & Explain
- Expressing this concept in a way you are able to handle, letting you take ownership of the information being passed through
- shows a deeper understanding of material
- Feinmann technique
- Questions
- Ask a lot of questions!
- Come up with a list of good questions about that video
- Questions that allow more deeper understanding
- Ask a lot of questions!
- Intrinsic Motivation
- Internal motivation
- Applied concepts, while nice, should also have intrinsic joy in concepts within mathematics
- Internal motivation
Example: Chess
- Growth Mindset: Improving is only upward!
- Metacognition: What parts of learning chess was effective/not?
- Simplify/Explain: Distill general principles of moves
- Questions: Why did they move this way? Why is this heuristic true?
- Intrinsic Motivation: want to do it for the game
Succeeding in Online Courses
- Practice math!
- Be as socially interactive as possible
- Do active assessment of your own learning capabilites, take record of what you understand and don’t
- Growth Mindset
- Work Hard, think of being a student like a profession
Tips to Make Practice Effective!
- Be Concept Focused!
- Sense-making: think about why the concept works and what’s going on
- Big Picture
- Try to see how that problem makes sense with your intuitive idea of how the concept works
- Make Predictions
- tweak problems to see trajectories on how these problems work
- Spaced Practice
- Do problems that recall information from before and improve long-term retention
- Do a bunch of little studying over a long period of time
- Interleaving
- Mix problems from other sections and multiple sections. Diversity in problem set allows for better long-term retention!
9 Tips to Prove Math Theorems
- Identify Logical Structure
- Conditional Statement, Biconditional Statement
- Proof Methods
- Direct Proof: assume p, conclude q
- Contrapositive: assume ~q, conclude ~p
- Contradiction: assume p, and ~q, and get a contradiction
- Counterexample: Find p that implies ~q
- Write Down Definitions!
- Aim for the Conclusion!
- Wherever you start, aim to get to the conclusion!
- Understand what the proof is saying
- What does this connection look like or mean? Get a large scale understanding
- Geometric Picture?
- Can you draw a picture that interprets the assumptions or conclusion?
- Concrete Example
- Valuable in understanding why the conclusion might be connected to the assumption
- Relevant Theorems?
- What are major theorems in a course?
- Read proofs of relevant theorems
- Play Around!
- Encourage proving things as an iterative process–growth mindset!
- Going down a rabbit hole and trying many things may lead to the solution
How to Watch Math Videos
- Investigate purpose (foundational knowledge)
- Pause/Rewind/Master
- Taking notes: Reflecting on your own notes
- Summarize
- Test yourself
- Be engaged
- Spaced out learning
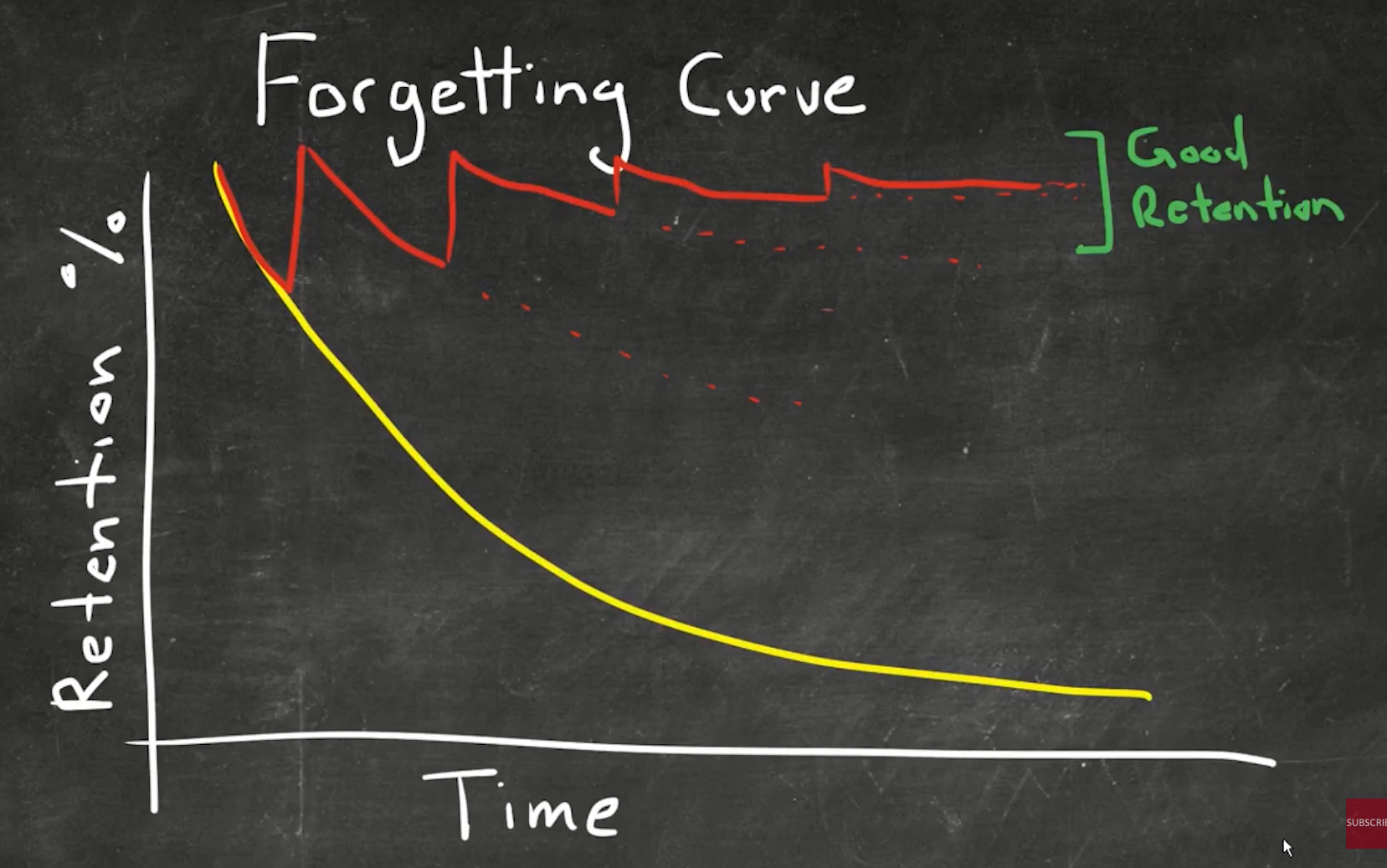
How to use Spaced retrieval to Memorize Facts!
- Spaced Retrieval Practice
- Forgetting Curve have an attenuation time
