Computational Methods: MATLAB
SLO:
- Use MATLAB as a computational tool to solve problems in engineering, mathematics, and the sciences.
- Use MATLAB as a plotting and visualization tool.
- Design, implement, and test computer programs to achieve stated objectives.
- Begin to use standard data structures.
- Working from a verbal or equation-based description, set up systems of simultaneous equations and use MATLAB to determine existence and uniqueness of solution and solve.
- Working from a verbal or equation-based description, use appropriate numerical techniques for differentiation, integration, and solution of differential equations.
- Apply numeric techniques and computer simulations to analyze and solve problems in engineering, mathematics, and the sciences.
Matlab vs Octave
- in Matlab,
%%is used to comment out code. However, in Octave, its##
Computational Methods: Octave/Matlab
Background
- compiled languages vs interpreted
- compiled require a programs code to be compiled before execution (specific to the processor)
- interpreted means an interpreter (more applicable across systems) will read high-level statements and execute the operation so on and so forth
- MATLAB is an interpreter!
- whitespace is not interpreted in Matlab
Common Commands:
clc: clears command window clear: clears all vars diary: records command terminal content exit: exits session who: prints all vars in workspace whos: ^^ but also prints size, bytes, class, etc ctrl-c: interrupts program format long/short: 15 digits and 4 digits respectivelyformat compact/loose: single and double spacing
Binary
- 0000, 0001, 0010…
- signed vs unsigned:
- unsigned represent non-negative values (1111 = 15)
- signed uses leftmost bit to represent positive of negative
- Binary has an additive property:
0 1 1 1
+ 0 1 1 0
= 1 1 0 1
- overflow: when a binary operator is too large to fit in bits. i.e. 10000 > 1111 + 0001
Variables and Assignments
- variable is a place for a programmer to store data in memory
- variables take on the value of its most recently assigned value. They can change!
Identifiers
| Keywords | |||
|---|---|---|---|
| break | else | global | return |
| case | elseif | if | spmd |
| catch | end | otherwise | switch |
| classdef | for | parfor | try |
| continue | function | persistent | while |
- The above CANNOT be used as identifiers
- as well as predefined mathematical constants, or functions
- Invalid:
$,-, starting with numbers,
- make meaningful names for variables
- Good Practice:
camelCasewith nounder_Scores
Numeric Variables
-
1 byte = 8 bits
-
Scientific Notation: $3.14 * 10^n$
- binary normalized scientific notation: $$ 1.f * 2^{exponent} $$
-
i.e. $1.010 * 2^5$
-
mantissa: the part of a floating-point number that represents the significant digits of that number, and that is multiplied by the base raised to the exponent to give the actual value of the number.
-
double precision, consisting of:
- 1 bit (bit 63) for the sign. 0 indicates the number is positive. 1 indicates the number is negative.
- 11 bits (bits 62 to 52) for the exponent.
- 52 bits (bits 51 to 0) for the fractional part of the mantissa; the whole part of the mantissa is always 1 and thus is not explicitly stored.
- range: $10^{308}$
-
The standard also defines a 32-bit floating-point representation known as single precision, with 1 bit for the sign, 8 bits for the exponent, and 23 bits for the fractional part
- range: $10^{38}$
-
realmax= $supernum$ -
realmin= $minimum$ -
MATLAB Defaults:
- creates real and double-precision numbers
Numeric Expressions
- do not omit th *
- minus used as a negative is known as unary minus
Precedence:
P(arenthesis ())
E(xponents ^)
M(inus signs, or ~ negations)
M(ultiplication * or)
D(ivision /)
A(ddition + or)
S(ubtraction -)
R(elational operators ==,<,>,<=,>=)
&
|
&&
||
- and left to right
- continuation (
...):
>> x1 = (1/2)^1+(1/2)^2+(1/2)^3+...
(1/2)^4+(1/2)^5+(1/2)^6+...
(1/2)^7+(1/2)^8+(1/2)^9;
- Good practice is to refrain from using very long expressions, instead breaking the expression into subexpressions by using intermediate variables, which makes the program more readable and easier to troubleshoot.
- reduce clutter
- The value Inf, meaning infinity, arises either when a nonzero value is divided by zero or when a mathematical expression results in an overflow. Overflow occurs when the result of a expression exceeds the maximum value that can be stored within a variable.
- The value NaN, meaning not-a-number, is generated by trying to evaluate expressions that do not have well defined mathematical values. For example, the expressions 0/0 and Inf-Inf evaluate to NaN.
String Scalars
- A string scalar stores text in a variable that has a class string.
- The ASCII standard is a commonly-used way of encoding characters using bits. For example, the 8-bit ASCII encoding of the character “s” is 1110011, which is 115 in decimal. The statement myChar = “s”
Logical Variables
- A logical value, also known as a Boolean value, can be only true (indicated by a non-zero number, typically 1) or false (indicated by the number 0)
- Such variables only occupy one byte each, in contrast to the numerical variable num, which occupies 8 bytes
xor(A, B): checks if truth value is the same
Short-Circuit Evaluation
- short-circuits occur when the rest of the logical operator is not executed, hence ‘short circuit’
&&:- 1st expression
true, 2nd expression evaluated - 1st value
false, 2nd expression isn’t
- 1st expression
||:- 1st expression
true, so 2nd expression isn’t evaluated - 1st
false, 2nd is evaluated
- 1st expression
Precendence
- Arithmetic operators (+, -, *) have precedence over relational operators
- == has precedence over &
Scripts
Functions
- Matlab has reusable functions
ismembertol(<calculation>,<goal>,<range>)
Modular Arithmetic
num0 % num1
This is equivalent to the remainder of $num0/num1$
Numeric Data-types
double floatis the most common floating-point type- A
double’s mantissa is limited to 16 digits (due to the number of bits that represent the mantissa), but an int’s range is about +/- 2 billion which means 10 digits.
linspace(<starting value>, <ending value>, <total partitions>)
logspace(<starting 10^n>, <ending 10^n>, <total partitions>)
//-TRIG-//
MATLAB function Description
sin Sine.
sind Sine of argument in degrees.
asin Inverse sine.
asind Inverse sine, result in degrees.
cos Cosine.
cosd Cosine of argument in degrees.
acos Inverse cosine.
acosd Inverse cosine, result in degrees.
tan Tangent.
tand Tangent of argument in degrees.
atan Inverse tangent.
atand Inverse tangent, result in degrees.
atan2 Four quadrant inverse tangent.
sec Secant.
secd Secant of argument in degrees.
asec Inverse secant.
asecd Inverse secant, result in degrees.
csc Cosecant.
cscd Cosecant of argument in degrees.
acsc Inverse cosecant.
acscd Inverse cosecant, result in degrees.
cot Cotangent.
cotd Cotangent of argument in degrees.
acot Inverse cotangent.
acotd Inverse cotangent, result in degrees.
//-HYPERBOLIC-//
sinh Hyperbolic sine.
asinh Inverse hyperbolic sine.
cosh Hyperbolic cosine.
acosh Inverse hyperbolic cosine.
tanh Hyperbolic tangent.
atanh Inverse hyperbolic tangent.
sech Hyperbolic secant.
asech Inverse hyperbolic secant.
csch Hyperbolic cosecant.
acsch Inverse hyperbolic cosecant.
coth Hyperbolic cotangent.
acoth Inverse hyperbolic cotangent.
//-EXPONENTIAL-//
exp Exponential.
log Natural logarithm.
log10 Common (base 10) logarithm.
sqrt Square root.
nthroot Real n-th root of real numbers.
Commonly-used formatting operators.
Operator Prints Description
%f
fixed-point f is for fixed-point.
%d
integer d is for decimal integer. The use of d is due to historical reasons, and is slightly misleading because a decimal number could have a fractional part. In MATLAB, %d means decimal integer which does not have a fraction.
%i
integer i is for integer. This operator is identical to %d when formatting output.
%c
character c is for character.
%s
string s is for string.
Commonly-used special characters.
Special character Description
\n
Prints a new line.
''
Two single quotation marks print a single quotation mark. Note that a single quotation mark alone would instead indicate the end of the format specification.
%%
Two percent characters print one percent character. Note that a single % character would instead indicate the start of a formatting operator like %f.
\\
Two backslash characters print one backslash character. Note that a single backslash character would instead indicate the start of a special character sequence like \n.
\t
Prints a tab.
Floating-point number formatting operators.
Operator Description
%f
Fixed-point notation
%e
Scientific notation with lowercase e, as in 3.141593e+00
%g
Either %f or %e, whatever is shorter
%E
Scientific notation with capital E, as in 3.141593E+00
%G
Either %f or %E, whichever is shorter
Conversion specification Description
-
Specifies left-justified display. Without this item, the default is right-justified.
fieldWidth
Number that specifies the minimum number of digits that will be displayed. If the actual number of digits is less, spaces are automatically inserted to reach the minimum. If not set, the number of digits corresponds to the default number digits used in the base workspace for the class of numeric variable (for more information, enter 'help format' on the command line).
precision
Number that specifies the number of digits to the right of the decimal point.
1D arithmetic array operators.
Element-wise operator Equivalent function Description
+
plus(a,b)
Addition
-
minus(a,b)
Subtraction
.*
times(a,b)
Element-wise array multiplication
.^
power(a,b)
Element-wise array exponentiation
./
rdivide(a,b)
Element-wise array division
ceil(n): rounds n upward
Indexing rows and Columns: Single Colon
MATLAB supports a single colon index to access all elements of a row or column. All of the third row can thus accessed as sampleMatrix(3, : ). Likewise, all of column 2 can be accessed as sampleMatrix( :, 2)
Concatenation
- Good practice is to use concatenation to create 2D arrays from 1D arrays, rather than creating one large 2D array. As shown above, monthSpend is created by concatenating weekSpend 1d arrays, rather than as an initial large 2D array.
Branching
- if-else
- switch-case: tests equality
- try-catch: handles errors
While and For Loops
i = 0;
while (i <= 99)
% Loop body statements go here
i = i + 1;
end
///////
for i=0:1:99
% Loop body statements go here
end
cellArrayOut = cell(numRows,numCols)
- cell creates a numRows × numCols cell array of empty cells. Cell arrays of higher dimensions can be created by calling cell() with additional arguments.
Review
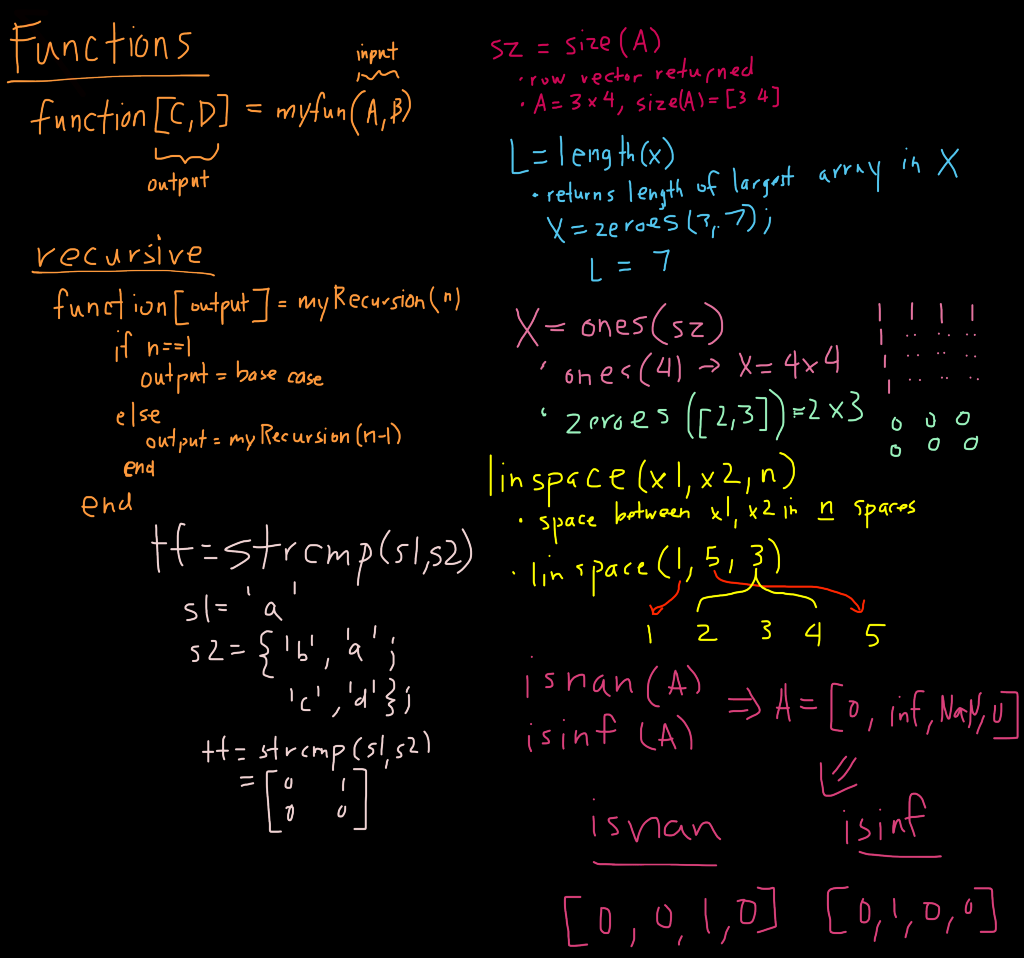
-
return causes an immediate end of a function
-
continue skips remaining statements in one iteration but doesnt end the loop
-
break terminates a loop and executes code after the ending statement corresponding to the interrupted loop
-
logical array is output when comparing two matrices with
== -
Newton Rhapson Method
-
Secant Method
-
fzero
-
roots(p)
Plotting
$ln(y) = m*x+ln(b)$ find the linear regression of the cubic, quadratic, and exponential of this data:
x = 1:4;
y = [45;5.3;0.76;0.09];
r2 = @(y, yH) 1 - sum(y-yH).^2 / sum(y-mean(y)).^2
% Finding the line
X_lin = [x', ones(length(x),1)];
B_lin = x_lin\y;
Y_linFit = @(x) B_lin(1) * x + B_lin(2);
B_linPoly = polyfit(x,y,1);
Y_linPolFit = polyval(B_linPoly, x_fit);
% Exponential
X_exp = [x', ones(length(x),1)];
B_Exp = X_exp\log(y);
Y_expFit = @(x) exp(B_Exp(2))*exp(B_Exp)*x);
B_ExpPoly = polyfit(x, log(y), 1);
Y_expFitPoly = polyval(B_ExpPoly, x)
Quadratic
Cubic
Exponential
ODE
2nd or 3rd ODE Reduce
